Publications
| International Journals |
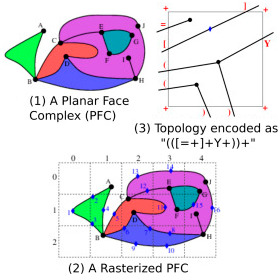
| Rasterized Planar Face Complex Damiand G., Rossignac J. Computer-Aided Design (CAD), Volume 90, pages 146-156, September 2017
Abstract: We consider a Planar Face Complex (PFC). It is defined by the immersion of a planar and connected graph G, which comprises a set of vertices joined by curved edges. G decomposes the plane into faces that need not be manifold or open-regularized and may be bounded by a single loop edge. The PFC may, for example, be used to represent the complex street network of a city, the decomposition of a continent into countries, or the inhomogeneous structure made of a large set of regions of different materials possibly with internal cracks. The rasterized Planar Face Complex (rPFC) proposed here provides a compact representation of an approximation of a PFC, where the precise location of each vertex is quantized to the pixel that contains it and where the precise geometry of each curved edge is approximated by the ordered list (with possible repetitions) of the pixels traversed by (a chosen polygonal approximation of) the edge. We claim three key contributions: (1) The geometric error between a PFC and its rPFC is bounded by the pixel half-diagonal. (2) In spite of such a drastic discretization of the geometry, the rPFC captures the exact topology of the original PFC (provided that no street lies entirely inside a single pixel) and supports standard graph traversal operators that permit to walk the loop of sidewalks along the streets that bound a face, to cross a street to the opposite sidewalk, or to cross streets in order while walking around their common junction. (3) The local connectivity and order information needed to provide the above functionality is stored at each pixel using only about 4 bits per crossing. We discuss the details of this representation, our implementation of its exact construction, four possible embodiments that offer different space/time efficiency compromises, experimental results, relations between rPFC and prior solutions. |
   |
 |
| Hierarchical Representation for Rasterized Planar Face Complexes Damiand G., Gonzalez-Lorenzo A., Rossignac J., Dupont F. Computers & Graphics (C&G), Volume 74, pages 161-170, August 2018
Abstract: A useful example of a Planar Face Complex (PFC) is a connected network of streets, each modeled by a zero-thickness curve. The union of these decomposes the plane into faces that may be topologically complex. The previously proposed rasterized representation of the PFC (abbreviated rPFC) (1) uses a fixed resolution pixel grid, (2) quantizes the geometry of the vertices and edges to pixel-resolution, (3) assumes that no street is contained in a single pixel, and (4) encodes the graph connectivity using a small and fixed number of bits per pixel by decomposing the exact topology into per-pixel descriptors. The hierarchical (irregular) version of the rPFC (abbreviated hPFC) proposed here improved on rPFC in several ways: (1) It uses an adaptively constructed tree to eliminate the “no street in a pixel” constraint of the rPFC, hence making it possible to represent exactly any PFC topology and (2) for PFCs of the models tested, and more generally for models with relatively large empty regions, it reduces the storage cost significantly. |
   |
 |
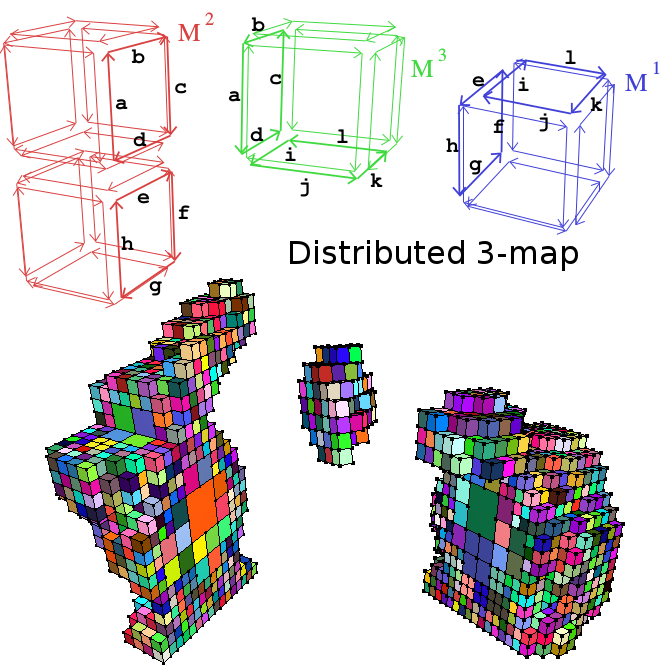
| Distributed Combinatorial Maps for Parallel Mesh Processing Damiand G., Gonzalez-Lorenzo A., Zara F., Dupont F. Algorithms, Volume 11, Number 7, August 2018
Abstract: We propose a new strategy for the parallelization of mesh processing algorithms. Our main contribution is the definition of distributed combinatorial maps (called n-dmaps), which allow us to represent the topology of big meshes by splitting them into independent parts. Our mathematical definition ensures the global consistency of the meshes at their interfaces. Thus, an n-dmap can be used to represent a mesh, to traverse it, or to modify it by using different mesh processing algorithms. Moreover, an nD mesh with a huge number of elements can be considered, which is not possible with a sequential approach and a regular data structure. We illustrate the interest of our solution by presenting a parallel adaptive subdivision method of a 3D hexahedral mesh, implemented in a distributed version. We report space and time performance results that show the interest of our approach for parallel processing of huge meshes. |
   |
 |

